С математикой по жизни

Уважаемые коллеги!

Возможно, вас удивило наличие на нашем Форуме данной темы по математике, поэтому я поясню причину ее появления.

В 2014 году я опубликовал на YouTube видеоролик "Видеонаблюдение: как оценить мертвую зону под видекамерой".

Сравнительно недавно в комментариях под этим видео я прочел упоминание об уроках математики… и задумался.

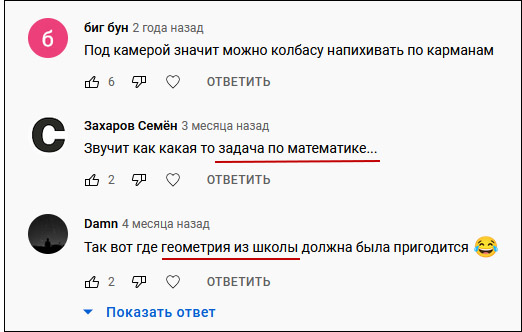
Дело в том, что более 40 лет назад я действительно преподавал математику на подготовительных курсах в ленинградском институте, который назывался СЗПИ.

Потом не раз в жизни я понемногу занимался с детьми (которых родители считали неспособными к математике), и ребята начинали приносить из школы пятерки.

Признаюсь, я люблю математику:

• в книгах по ремонту телевизоров я, наверное, единственный автор в этой области, кто рассмотрел процесс поиска неисправности с помощью основ теории вероятности и теории информации;
• в книге "Охранное телевидение" я широко использовал геометрию и тригонометрию;
• рассчитал и создал телевизионные испытательные таблицы;
• подготовил расчеты онлайн (фокусное расстояние объектива, диагональ монитора, перевод дюймов в сантиметры, выбор длины проводов и пр.).

"Почему бы не стать репетитором?" - сказал я себе. Действительно, детей я люблю, умею им доступно объяснять, с родителями смогу найти общий язык.

И вот для чего я это всё написал.

Коллеги! У меня ко всем просьба: если у вас (или у ваших знакомых) есть дети или внуки (желательно с 5 по 11 класс), с которыми нужно заниматься по математике, то я готов помочь.

Занятия я провожу дистанционно – по Skype или ZOOM.

Подробности по e-mail: yurigedzberg@gmail.com

Я решил прокомментировать данную задачу.

Для начала приведу чертеж, более реальный к действительности (по сравнению с исходным чертежом, в котором пропорции нарушены, возможно, сознательно, чтобы усложнить решение задачи).

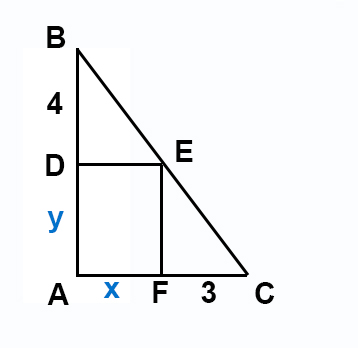
Найти площадь прямоугольника ADEF со сторонами x и y достаточно просто, составив пропорцию сторон из любой пары трех подобных треугольников: ABC, DBE, FEC, например, так:

4 / y = x / 3

Откуда площадь ADEF:

S_ADEF = x * y = 4 * 3 = 12

Отсюда одну сторону можно выразить через другую:

y = 12 / x

Искомая площадь треугольника ABC:

S_ABC = S_DBE + S_ADEF + S_FEC = (1 / 2) 4 * x + x * y + (1 / 2) y * 3 = (1 / 2) 4 * x + 12 + (1 / 2) * (12 / x) * 3 = 2 x + 12 + 18 / x

Берем производную:

S'_ABC = 2 – 18 / x²

Приравниваем ее нулю и преобразуем:

2 x² = 18

Горизонтальная сторона прямоугольника ADEF: x = 3 (отрицательный корень отбрасываем).

Вертикальная его сторона: y = 12 / 3 = 4

Соответственно, минимальная площадь треугольника ABC (при заданных условиях):

S_ABC = (1 / 2) 4 * 3 + 12 + (1 / 2) 4 * 3 = 24

Это действительно минимум функции:

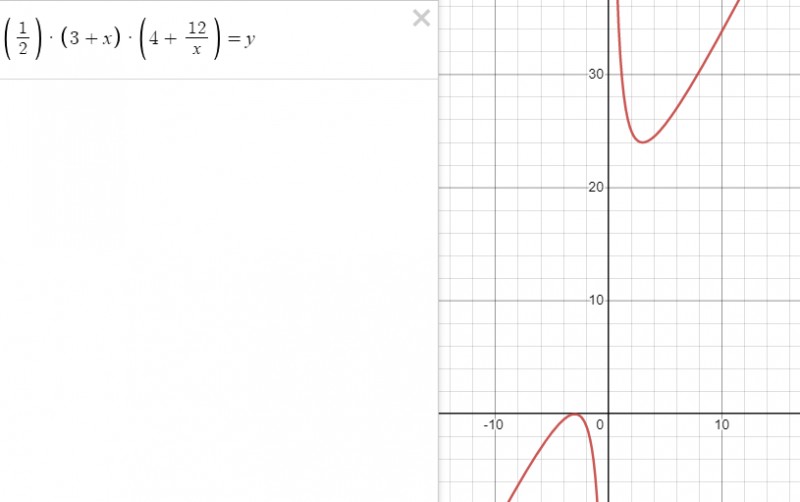
По сути, все это есть в видеороликах.

Нет в них лишь нескольких моментов.

1. Вершины прямоугольника оказываются на серединах сторон треугольника ABC.

2. Проведем диагональ в прямоугольнике DF, которая делит треугольник ABC на 4 одинаковых прямоугольных треугольника (кстати, это так называемые Пифагоровы тройки со сторонами 3, 4, 5).

3. Поэтому для вычисления площади треугольника ABC достаточно вычислить площадь одного маленького треугольника и результат умножить на 4:

(1 / 2) 4 * 3 * 4 = 24

Аналогичный результат можно получить из подобия треугольников ADF и ABC, площади которых пропорциональны коэффициенту подобия в квадрате, то есть 2² = 4. Тот же результат получается, если взять удвоенное значение площади прямоугольника.

4. Главный вывод: совсем не обязательно подробно решать подобную задачу – ответом является удвоенное произведение указанных в условии отрезков сторон:

S_ABC = 2 * 4 * 3 = 24

Возникает вопрос: насколько случайны совпадения: на стороне AB имеются рвные отрезки 4 и 4, на стороне AC отрезки 3 и 3?

Обозначим дополнительные отрезки на этих сторонах как a и b

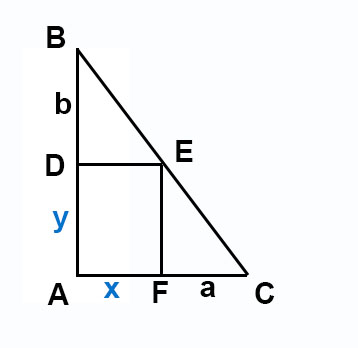
Повторим расчет в общем виде.

b / y = x / a

x * y = a * b

S_ABC = (1 / 2) b * x + a * b + (1 / 2) a * (a * b) / x

Берем производную и приравниваем ее нулю:

(1 / 2) b - (1 / 2) a² * b / x² = 0

x² = a²

x = a

Аналогично можно получить y = b

События независмые, поэтому вероятности перемножаются:

P = 0,006 * 0,04 = 0,00024

3D, говорите? Ну-ну...

Вот старинный учебник по геометрии 1570 года:

Все уже когда-нибудь было.

Эта задача со стремянкой, мне кажется, может служить хорошей иллюстрацией, что графические решения подчас являются более наглядными и более эффективными, чем аналитические:

Я поступил следующим образом.

1. Из подобия маленьких треугольников составил пропорцию:

y / 1 = 1 / x

Отсюда y = 1 / x (функция обратно пропорциональной зависимости, ее график - гипербола)

2. Для большого треугольника (благодаря Пифагору) можно записать:

(x + 1)² + (y + 1)² = 4² (это уравнение окружности радиуса 4)

Вводим данные в сервис Desmos, ву-а-ля:

Точки пересечения графиков в области положительных чисел - это решения задачи:

x₁ = 0,362 y₁ = 2,761

x₂ = 2,761 y₂ = 0,362

Есть возможность померяться интеллектом с Альбертом Эйнштейном.

Задача

Машина прошла 1 милю со скоростью 15 миль в час. С какой скоростью она должна пройти следующую милю, чтобы средняя скорость на этих 2 милях была 30 миль в час?