Страницы нашей жизни / Жизнь - это не только работа /
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
13.07.2022 08:38:09
Уважаемые коллеги!
Возможно, вас удивило наличие на нашем Форуме данной темы по математике, поэтому я поясню причину ее появления.
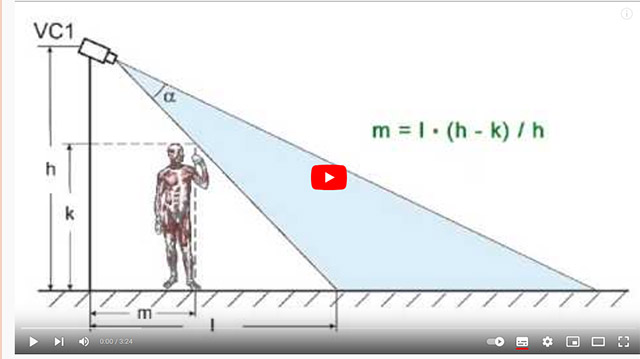
В 2014 году я опубликовал на YouTube видеоролик "Видеонаблюдение: как оценить мертвую зону под видекамерой".
Сравнительно недавно в комментариях под этим видео я прочел упоминание об уроках математики… и задумался.

Дело в том, что более 40 лет назад я действительно преподавал математику на подготовительных курсах в ленинградском институте, который назывался СЗПИ.
Потом не раз в жизни я понемногу занимался с детьми (которых родители считали неспособными к математике), и ребята начинали приносить из школы пятерки.
Признаюсь, я люблю математику:
- в книгах по ремонту телевизоров я, наверное, единственный автор в этой области, кто рассмотрел процесс поиска неисправности с помощью основ теории вероятности и теории информации;
- в книге "Охранное телевидение" я широко использовал геометрию и тригонометрию;
- рассчитал и создал телевизионные испытательные таблицы;
- подготовил расчеты онлайн (фокусное расстояние объектива, диагональ монитора, перевод дюймов в сантиметры, выбор длины проводов и пр.).

"Почему бы не стать репетитором?" - сказал я себе. Действительно, детей я люблю, умею им доступно объяснять, с родителями смогу найти общий язык.
И вот для чего я это всё написал.
Коллеги! У меня ко всем просьба: если у вас (или у ваших знакомых) есть дети или внуки (желательно с 5 по 11 класс), с которыми нужно заниматься по математике, то я готов помочь.
Занятия я провожу дистанционно – по Skype или ZOOM.
Подробности по e-mail: yurigedzberg@gmail.com
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
13.07.2022 08:39:52
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
14.07.2022 06:42:20
a + b = c
Значит:
a + b - c = 0
Уж сколько раз твердили миру: "На нуль нельзя делить, нельзя!".
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
14.07.2022 21:03:20
Узнал, что существует более 400 доказательств теоремы Пифагора.
И это впечатляет.
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
15.07.2022 07:05:14
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
16.07.2022 08:13:12
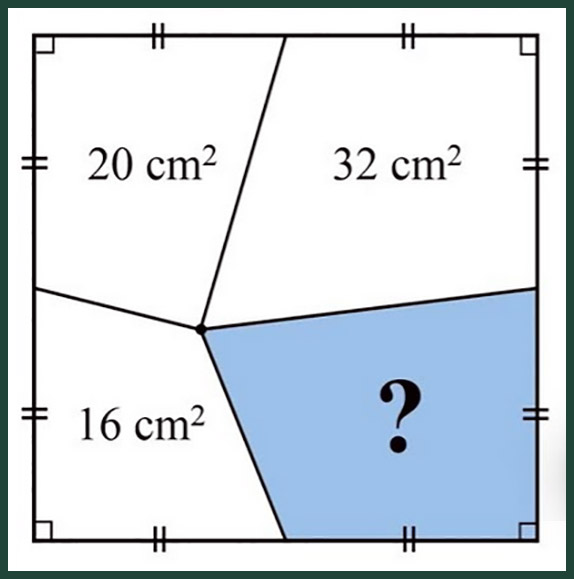
Чему равна площадь, выделенная голубым цветом?
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
17.07.2022 20:22:40
Я решал эту задачу довольно просто.
Для начала соединил общую точку всех участков с вершинами квадрата - получилось 4 треугольника. В каждом из треугольников границы участков являются медианами, а это значит, что они делят каждый из треугольников на два равновеликих (то есть имеющих равные площади треугольника).
Для определенности одну из площадей голубого участка я обозначил за x.
Тогда нижний треугольник можно представить состоящим из двух равновеликих треугольников (левого и правого) с площадями, равными х.
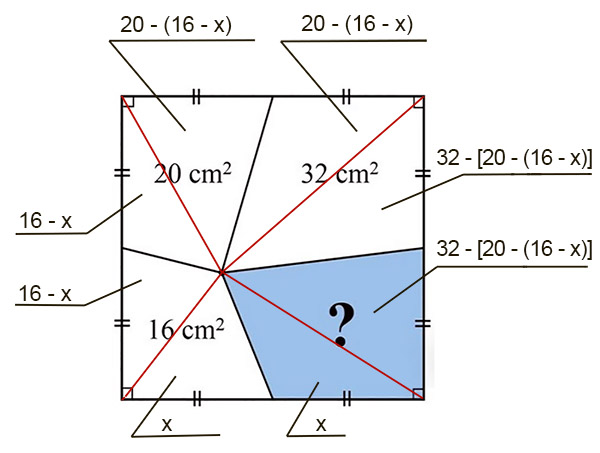
В этом случае большой левый треугольник можно представить состоящим из левого нижнего треугольника и левого правого. Очевидно, что площадь левого нижнего треугольника равна 16 - х. Значит, и площадь левого треугольника также равна 16 - х.
Рассуждая подобным образом можно сделать вывод, что верхний треугольник делится медианами на два равновеликих треугольника с площадями 20 - (16 - х).
Аналогично, правый треугольник можно представить состоящим из двух треугольников с площадями 32 - [20 - (16 - х)].
Тогда искомая площадь голубого участка:
x + 32 - [20 - (16 - х)] = x + 32 - 20 + (16 - х) = x + 32 - 20 + 16 - х = 28
Конечно, Борис Трушин предложил более изящное решение этой задачи:
.
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
18.07.2022 13:27:09
Найти недостающие цифры:
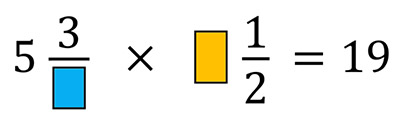
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
19.07.2022 07:47:05
Я решал так.
Оба сомножителя представляют собой смешанные числа (каждое состоит из целой части и правильной дроби).
Оценим возможные пределы нахождения сомножителей.
Первый сомножитель может иметь значения от (5 3/4) до 5 (при стремлении знаменателя дроби к бесконечности).
Тогда диапазон значений второго сомножителя получается делением произведения (19) на первый сомножитель, поэтому второй сомножитель может принимать значения от 3,304 до 3,8. Однако второй сомножитель содержит дробную часть, равную 1/2, поэтому он может быть равным только (3 1/2).
Тогда первый сомножитель находится делением 19 на второй сомножитель:
19 : (3 1/2) = 19 : (7/2) = 38 / 7 = (5 3/7)
Такой же результат можно получить и по-другому.
Произведение двух чисел равно 19 – это простое число (оно делится только на 1 и на самого себя). Стало быть, в левой части равенства один из двух искомых сомножителей при разложении их на множители обязательно должно содержать число 19.
Например, формально второй сомножитель может быть равным (9 1/2) = 19/2. Однако мы уже выяснили, что целая часть второго числа не должна превышать 3.
Поэтому в поисках множителя 19 следует обратить внимание на первый сомножитель – его знаменатель может быть равен 5, 6, 7… Однако, только при знаменателе, равном 7, числитель неправильной дроби становится кратным 19, а именно:
5 3/7 = 38/7 = (19*2) / 7
Если это так, то для получения в ответе числа 19 нужно, чтобы данная дробь сократилась на 2/7, то есть первый сомножитель надо умножить на число, обратное 2/7, а именно, на
7/2 = 3 1/2
Ответ:
5 3/7 х 3 1/2 = 19
У автора видеоролика примерно такие же рассуждения:
Юрий Гедзберг
Старожил
Сообщений: 8679
Рейтинг: 32616
20.07.2022 08:15:38
Говорят, что математика - это модель реальности, модель нашей жизни.
На эту сентенцию наталкивают математические фокусы подобные приведенному выше, когда делается недостоверное заявление, а потом, отталкиваясь от него, уже как от истины, начинается бурная работа (преобразования из пустого в порожнее: замены, подстановки, вычитания, возведения в степень и пр.) по принципу "кручу-верчу-запутать хочу".
Посмотрите начало "доказательства" этого фокуса, что 3 = 0:
Let x be a solution of x2 + x + 1 = 0
То есть делается вроде бы безобидное заявление: "Пусть (или допустим) x является решением уравнения x2 + x + 1 = 0".
Если вы это проглотили и читаете дальше, всё - вы уже на крючке, вам можно вешать любую лапшу.
- А что же делать?
- Как что? Стоп!!! И резко по тормозам. И вопрос - а где доказательства???
Ведь достаточно сделать простую проверку - вычислить дискриминант этого уравнения:
D = b2 – 4ac = 1 – 4 * 1 * 1 = - 3 < 0
И всё, дальше можно не продолжать, ведь дискриминант этого квадратного уравнения отрицательный, а это значит, действительных корней у него нет и не будет, так что никаких "Let x be a solution"!!! Все дальнейшие преобразования - это, простите, фуфло.
И если в математике подобные фокусы проверяются на раз, то в политике, в пропаганде ложь подчас сравнительно легко просачивается в наши головы благодаря нашей с вами лени потребовать доказательства каких-то заявлений или готовности отключить свое критическое мышление и вестись на любую ложь, особенно, если она служит подтверждением каких-то наших априорных предпочтений (давно уже вбитых кем-то в наши головы).
Например, читаешь заголовок: "Почему все ненавидят...". Казалось бы, сразу должен возникнуть законный вопрос, кто это "все", кто конкретно? Но если вы заинтригованы заголовком, если вас интересует только "почему", а остальное вы проглатываете, то вы уже на крючке.
Или еще один прием недобросовестных пропагандистов, зачин типа "Всем известно, что...". Вы читаете или слышите такое, и вам даже неловко поинтересоваться, а кому это "всем". Вы думаете, может, действительно все знают, а это я такой отсталый. Налицо дешевая манипуляция вашим сознанием.
Мораль сказанного:
не ведитесь на бездоказательные заявления - ни в математике, ни в жизни!