С математикой по жизни

Уважаемые коллеги!

Возможно, вас удивило наличие на нашем Форуме данной темы по математике, поэтому я поясню причину ее появления.

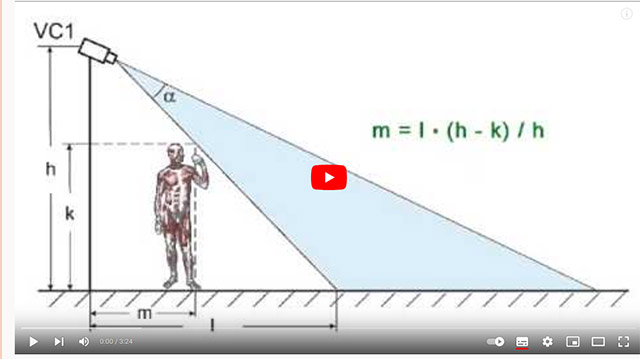
В 2014 году я опубликовал на YouTube видеоролик "Видеонаблюдение: как оценить мертвую зону под видекамерой".

Сравнительно недавно в комментариях под этим видео я прочел упоминание об уроках математики… и задумался.

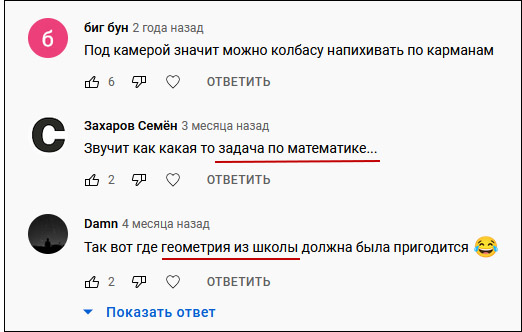
Дело в том, что более 40 лет назад я действительно преподавал математику на подготовительных курсах в ленинградском институте, который назывался СЗПИ.

Потом не раз в жизни я понемногу занимался с детьми (которых родители считали неспособными к математике), и ребята начинали приносить из школы пятерки.

Признаюсь, я люблю математику:

• в книгах по ремонту телевизоров я, наверное, единственный автор в этой области, кто рассмотрел процесс поиска неисправности с помощью основ теории вероятности и теории информации;
• в книге "Охранное телевидение" я широко использовал геометрию и тригонометрию;
• рассчитал и создал телевизионные испытательные таблицы;
• подготовил расчеты онлайн (фокусное расстояние объектива, диагональ монитора, перевод дюймов в сантиметры, выбор длины проводов и пр.).

"Почему бы не стать репетитором?" - сказал я себе. Действительно, детей я люблю, умею им доступно объяснять, с родителями смогу найти общий язык.

И вот для чего я это всё написал.

Коллеги! У меня ко всем просьба: если у вас (или у ваших знакомых) есть дети или внуки (желательно с 5 по 11 класс), с которыми нужно заниматься по математике, то я готов помочь.

Занятия я провожу дистанционно – по Skype или ZOOM; в Санкт-Петербурге могу приехать к ученику домой.

Подробности по e-mail: yurigedzberg@gmail.com

Самолет летел, например, из Москвы во Владивосток, а затем возвращался обратно - и все это время была безветренная погода.

Другой раз он летит тем же рейсом туда и обратно, но все это время дует ветер в одном направлении и одной силы - когда самолет летел в одну сторону, то ветер был встречным, а когда в другую сторону, то попутным.

В каком случае на дорогу уйдет больше времени?

Мой комментарий

Обозначим: весь путь S, скорость самолета Vс, скорость ветра Vв.

Тогда время в пути туда и обратно в безветренную погоду

Tб = 2S / Vс

Теперь летим в ветренную погоду.

Время на полет в одну сторону (по ветру):

Tпо = S / (Vс + Vв)

Время на полет в обратную сторону (против ветра):

Tпр = S / (Vс - Vв)

Общее время полета в оба конца в ветренную погоду:

Tв = Tпо + Tпр = S / (Vс + Vв) + S / (Vс - Vв) = 2 * S * Vс / ((Vс)² – (Vв²))

Tв = 2 * S / (Vс – Vв / Vс)

Что мы видим?

В безветренную погоду (Vв = 0) отношение Vв / Vс равно нулю, понятно, что Tб = 2S / Vс – это лишь частный случай (хорошей погоды). Во всех остальных случаях реальная скорость оказывается меньше, а время самолета в пути в оба конца больше, чем в безветренную погоду.

Казалось бы, почему? Ведь в одну сторону скорость увеличилась на определенную величину, зато в другую сторону она на столько же уменьшилась…

Дело вот в чем. Как мы помним, пройденный путь – это произведение скорости на время в пути, что выражается законом прямой пропорциональности: S = V * T (график этой функции – прямая, проходящая через начало координат под углом, тангенс которого численно равен скорости). И рассуждения, например, о среднем пройденном пути (в одну сторону скорость прибавили, в другую на столько же убавили) будут справедливы (об этом, например, существует целый пласт задач о движении катера в стоячей воде, по течению реки или против течения).

Все это так, однако такие рассуждения не справедливы для времени!

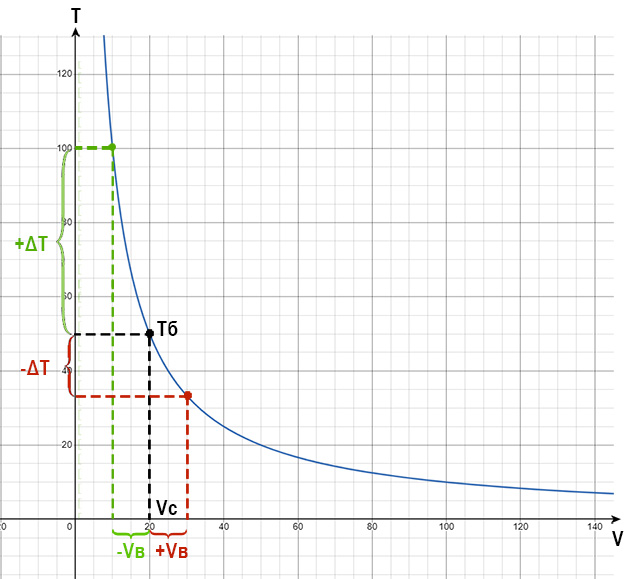
Потому что T = S / V – функция обратно пропорциональной зависимости, ее график гипербола. Для рассмотренных задач это убывающая функция, то есть приращение скорости и уменьшение скорости на одну на ту же величину дает различное уменьшение/приращение времени, причем, при увеличении скорости это уменьшение меньше, чем приращение времени при уменьшении скорости. То есть результирующе эти равные изменения скорости оказывают различное влияние на время. Вот поэтому суммарное время полета и возрастает.

Ну, что ж, как пелось в популярной песне:

"Летайте самолётами Аэрофлота,

Живите на лету.

А если вдруг нелётная погода,

Влюбитесь в аэропорту"

Я решал эту задачу по-другому.

Должны выполняться два условия:

x, y, z – числа натурального ряда (то есть целые положительные числа, не ноль)

для обозначения каждого из них используется лишь одна буква

Итак,

x + 1 / (y + 1 / z) = 10 / 7

Приводим к общему знаменателю в скобках:

x + z / (y * z + 1) = 10 / 7

Еще раз преобразуем:

(x * y * z + x + z) / (y * z + 1) = 10 / 7

Правая часть уравнения представляет собой неправильную дробь, но главное – несократимую дробь, числитель и знаменатель которой является взаимно простыми числами. То есть если бы x, y, z в левой части уравнения имели бы общие множители, то их можно было бы вынести за скобку в числителе и знаменателе и они бы сократились.

Поэтому исходное уравнение можно записать в виде системы уравнений:

x * y * z + x + z = 10

y * z + 1 = 7

То есть должны одновременно выполняться условия для x, y и z в каждом из этих двух уравнений.

Первое из этих уравнений можно записать следующим образом:

x * y * z = 10 – x – z

Максимальное значение произведения x * y * z = 7 (поскольку минимальная сумма x и z составляет 3, то есть это могут быть числа 1 и 2 (или 2 и 1).

Однако 7 – это простое число, которое не имеет других делителей, кроме 1 и 7, а значит, его нельзя разложить на множители x * y * z. Поэтому следующим для рассмотрения должно быть выбрано число 6, то есть x * y * z = 6 (а значит, сумма x и z равна 10 - 6 = 4)

При этом возможны следующие варианты множителей:

Что касается суммы x + z = 4, то она может быть реализована при следующих вариантах неизвестных:

Относительно второго уравнения y * z + 1 = 7 - его можно преобразовать: y * z = 6. Данные сомножители могут принимать следующие значения:

Однако последние два варианта значений 6 и 1 или 1 и 6 противоречат рассмотренным выше требованиям.

Если теперь рассмотреть перечисленные варианты, то единственным одновременно приемлемым для всех условий вариантом является следующий:

x = 1

y = 2

z = 3

Более простое решение.

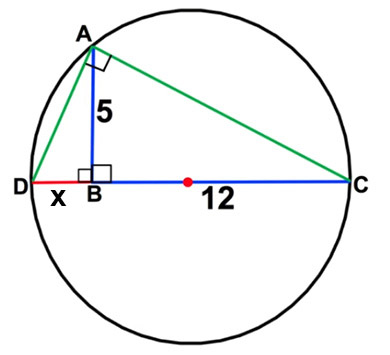
1. В прямоугольном треугольнике квадрат высоты на гипотенузу равен произведению отрезков гипотенузы, то есть AB² = DB * BC, то есть 5² = x * 12, откуда x = 25 / 12
2. Диаметр DC = DB + BC = 25 / 12 + 12 = 169 / 12
3. Радиус r = DC / 2 = 169 / 24